Background: CAMD of Critical Path Institute developed a quantitative model to describe the progression of cognitive changes in mild to moderate to test and optimize operating characteristics of trial designs for AD (via simulations based on the model). The model and the simulation tool got approval from FDA as “Fit for Purpose”. The original ADAS-cog progression model was based on Beta regression. However, as noted by Hahn (2008), Garcia et al. (2011), and Bayes et al. (2012), the Beta distribution considers neither the tail area events nor the outlying events, fails to represent excess variability and overoccurrence of tail-area events, which could limit its applications for modeling the proportional data (data in the open unit interval (0, 1) such as ADAS-cog score after being divided by 70). An alternative to the Beta distribution is the Beta rectangular (BR) distribution, which assigns more weight to extremal tail-area events and more probability to the outliers and extremal events. Specifically, the BR distribution has a shape parameter \theta (between 0 and 1) controlling the thickness of the tails. When, \theta = 0, the BR distribution reduces to the Beta distribution. In general, when 0<\theta <1, the BR distribution has heavier tails than its Beta distribution counterpart. Please refer to Figure 2 in Wang and Luo (2016) for a visual comparison of Beta and BR distributions.
In the analysis, I compared of the Beta regression model and Beta-rectangular regression model in describing the longitudinal progression of the ADAS-cog in AD patients. I used the testing data set (with ADNI study and 49 meta studies) provided in the tool development group web page, combining with the Study 1013 from Coalition Against Major Diseases (CAMD) database required from Critical Path Institute. The total observations were 6339 from 1005 subjects in 51 studies.
Results: The table below presents the mean of estimated posterior of parameters directly from BUGS models. The “Original Model” refers to the original Beta regression model. The “BR” refers to the Beta-rectangular model. The BUGS code for this Beta-rectangular model is provided [code].
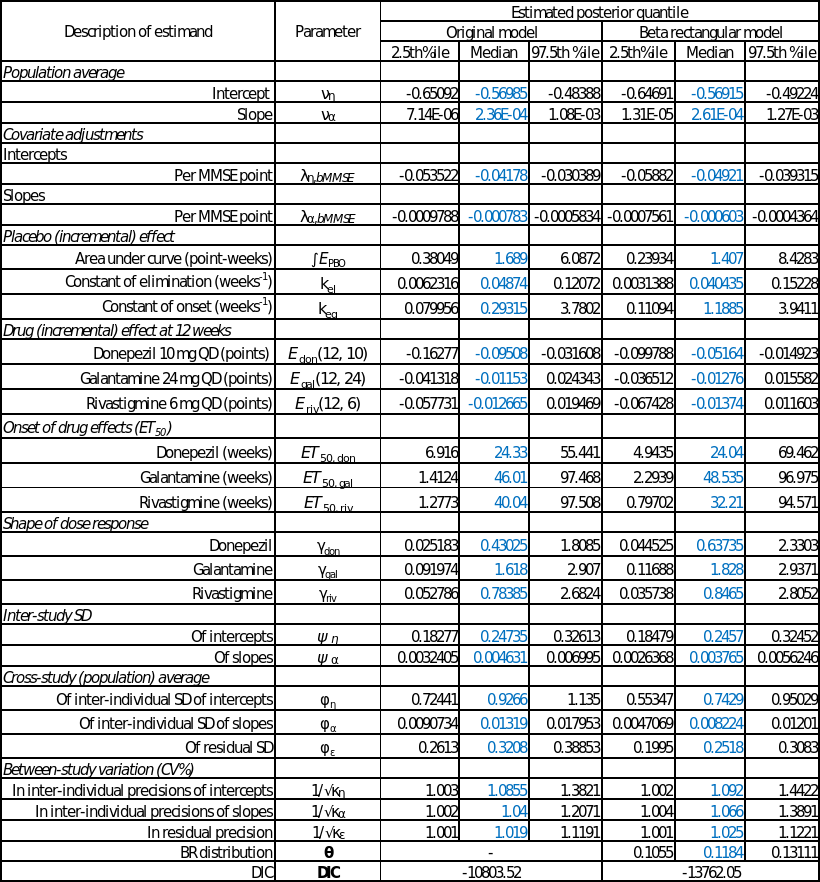
The table indicated that the shape parameter \theta = 0.1184 > 0, and the deviance information criterion (DIC, a Bayesian model selection tool and smaller values indicate a better model fit) in favor of the Beta-rectangular regression model over the Beta regression model. These facts suggested that BR model provided a better model fit in describing longitudinal progression of the ADAS-cog and the existence of potential outliers and heavier tails than what the Beta distribution can model. It worth to include more well processed clinical trial data to do further analysis.