Background: In particular, conventional MCMC algorithms are computationally very expensive for large data sets. A promising approach to solve this problem is embarrassingly parallel MCMC (EP-MCMC), which first partitions the data into multiple subsets and runs independent sampling algorithms on each subset. The subset posterior draws are then aggregated via some combining rules to obtain the final approximation. This work is testing the method of parallelizing MCMC with Random Partition Trees (PART) proposed by Xiangyu Wang and David Dunson ( [paper] , [code] ) in a simulation setting of a multi-level item response theory (MLIRT) model .
Methods: For the simulation study, I generate 100 datasets. Each dataset contain 1200 subjects with 7200 observations. There are 23 parameters need to be estimated. The dataset is randomly split into 6 subsets. For each subset chains, I run the MLIRT model [code] for 1000 iterations after 3000 burn-in. Thinning by 1 results in 1000 samples. The posteriors samples of each subset chain are aggregated by PART-KD. The results of PART are obtained with minimal cut length as 0.01, minimal fraction block as 0.1 and 10 trees. The model inference using 1200 subjects takes around 27 hours to finish, while each sub-chain (using 200 subjects) takes 2 to 3 hours to finish, and could be run in parallel. I repeat the process on all 100 datasets and obtain 100 copies of aggregated posterior each has 10000 samples.
Results:
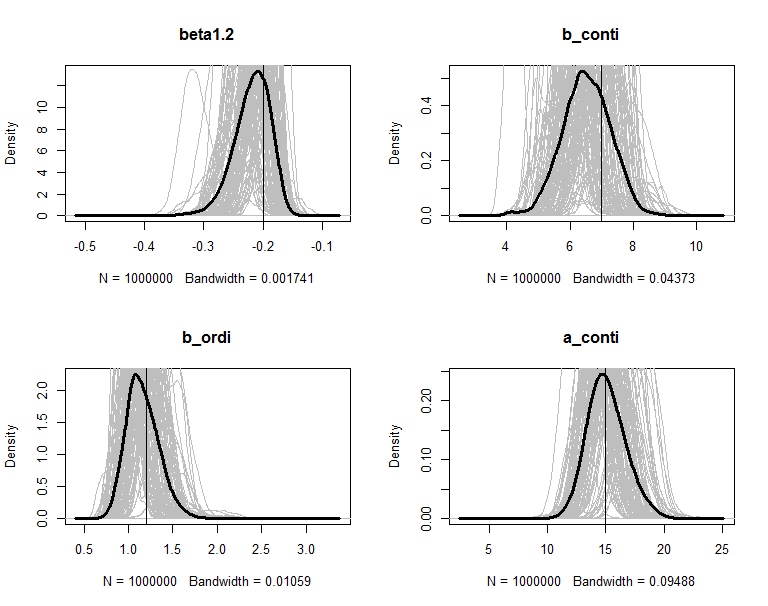
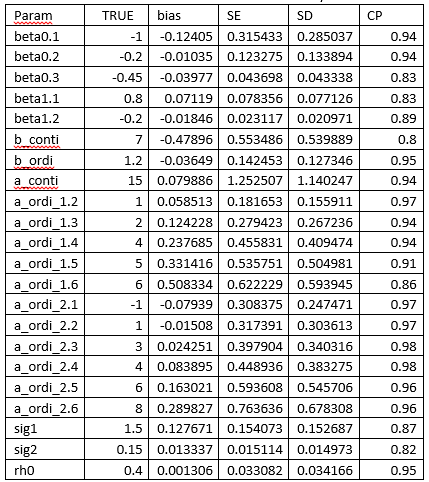
The simulation results is summarized in the blow table. Majority of the parameters have a small bias and the coverage probability is around 0.95.
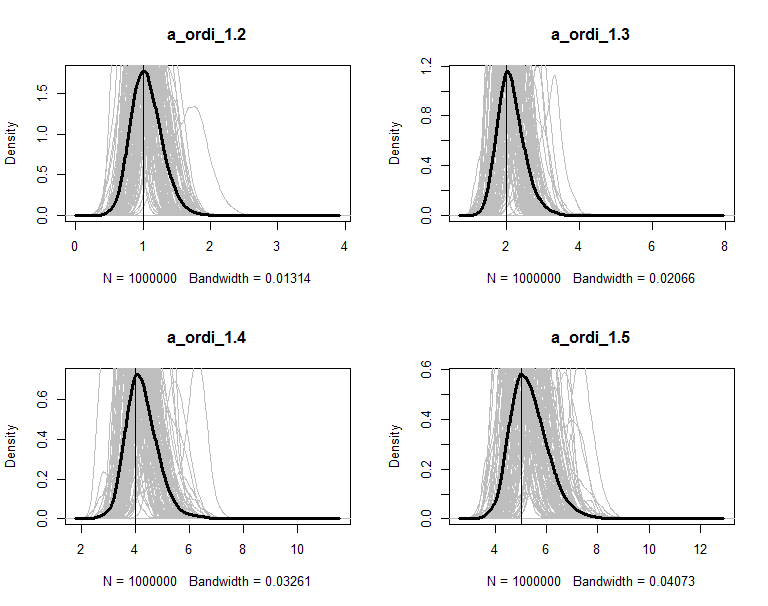
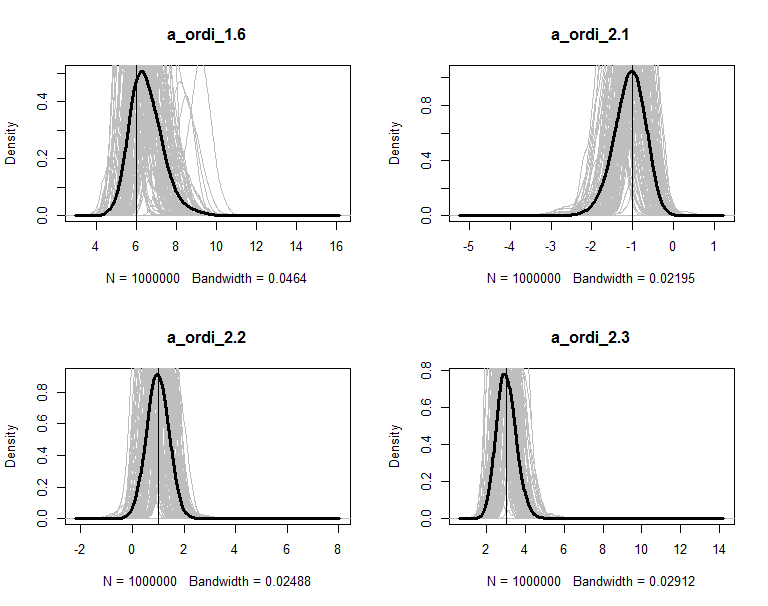
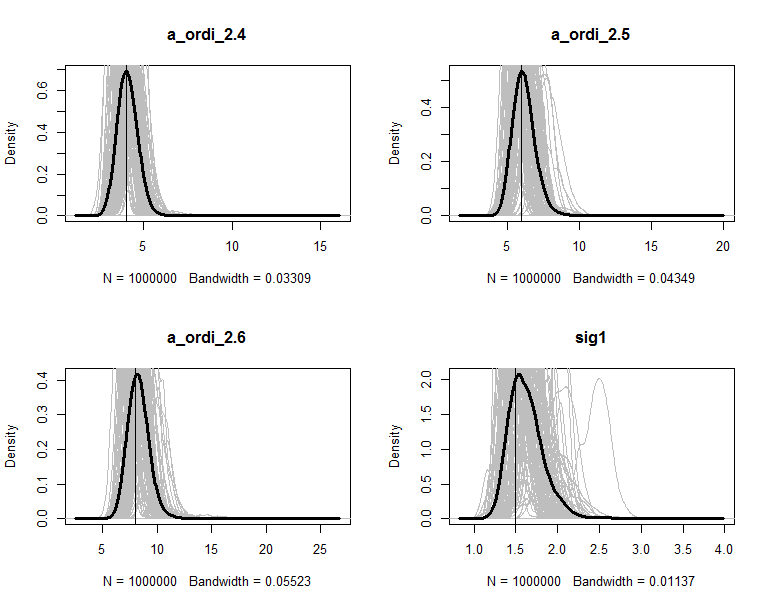
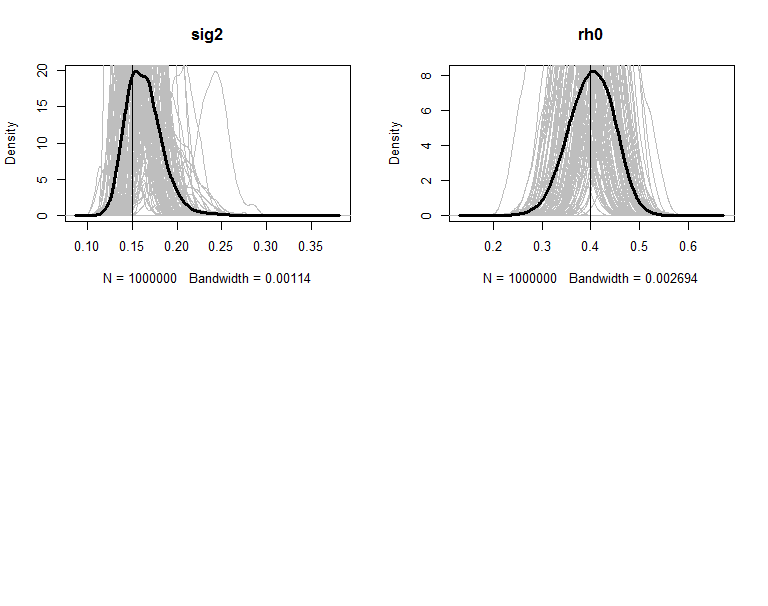
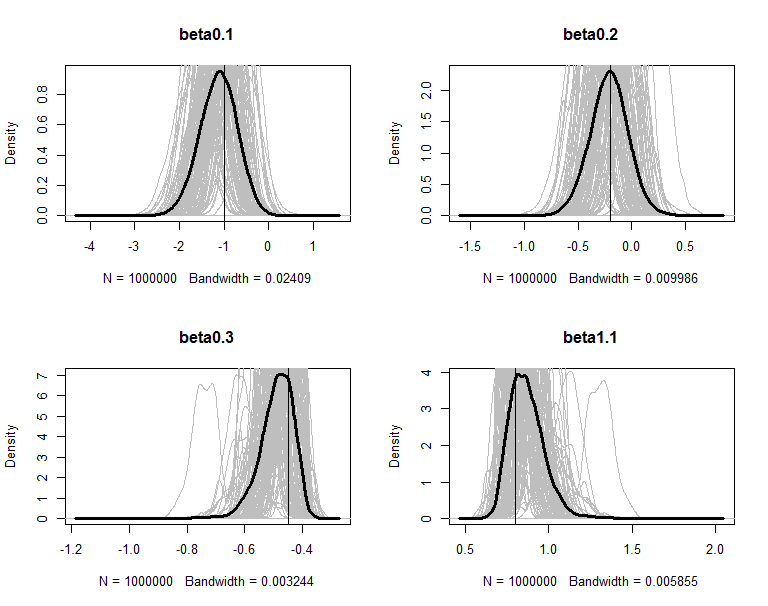
The posteriors are plot in figures. The grey lines are the density of 100 copies of aggregated posterior. The solid wide line is density of combine the 100 copies together. The vertical line is the true value of the parameter.
</span>
In conclusion, the PART method could dramatically decreases the computation time for Bayesian inference of large data set and provides relative good estimations (after aggregating sub-chains) in a moderate complex model.